Uniswap Labs月入百万美元 新收费模式领跑DeFi复苏
2023年11月17日,Fhenix发布了其全同态加密FHE-Rollups白皮书。这些Rollups可以实现安全的链上交易和私有应用程序,让开发人员能够构建机密的L2网络,同时保持与以太坊的兼容性。 金色财经0xjs编译了FHE-Rollups白皮书。
摘要
Fhenix引入了全同态加密(FHE)Rollup的概念:一种用于执行任意机密智能合约的更具可扩展性的技术。最近的研究表明FHE是为智能合约添加机密性的可行解决方案。然而,这些工作限制了可扩展性,因为它们需要网络中的所有节点执行 FHE计算并就加密状态达成共识。
受到以太坊生态系统中最近转向L2解决方案发展的启发,Fhenix提出了第一个基于FHE的Rollup架构。我们认为,FHE对于明文计算Rollup是一个必要的解决方案,尽管在FHE背景下,计算开销要高出几个数量级。
在我们的设计中,我们采用乐观Rollup方法,使我们能够避免由最先进的可验证FHE技术带来的数量级损失。事实上,我们的框架可以被视为解决同样问题的加密经济解决方案。
专注于以太坊生态系统,我们提出并克服了基础层仲裁非EVM原生欺诈证明的挑战。我们无需对以太坊进行任何更改即可实现这一目标,这表明以太坊上的原生FHE Rollup确实是可能的。我们构建了一个部分概念验证,使用Arbitrum的Nitro证明者和Zama的 tfhe-rs库来演示这一点。
一、引言
前言
这是Fhenix 关于 FHE Rollups 的“滚动白皮书”的第一个版本(v0.1)。它是一份有生命力的文件,我们会滚动更新和扩展,包括纳入来自我们不断壮大的社区以及外部研究人员的反馈。
区块链以信任最小化的方式(即不信任任何中心化运营商)确保正确执行和抗审查,但代价是数据机密性。本质上,链上的所有数据都是公开的,因为所有节点都需要看到数据才能达成共识。尽管普遍认为,这种极端的透明度只是系统的副产品,而不是系统的目标,而且它在很大程度上限制了我们可以构建的用例类型,因为我们无法构建任何需要利用敏感数据的应用程序。
近年来,研究人员和从业者在一系列被称为机密智能合约的工作中采用了多种隐私保护技术来解决区块链的机密性问题。在所有这些技术中,全同态加密(FHE)可能是最雄心勃勃的,因为它允许直接计算加密数据而无需解密。自从Gentry在大约十五年前提出第一个构造以来,FHE已经取得了突飞猛进的进步。尽管如此,与明文计算相比,FHE 需要大量的计算开销,这使得在L1执行不切实际,其中每个节点都需要复制整个计算,而这也是最先进的基于FHE 的机密智能合约框架正在采用的方法。
受到以太坊生态系统中最近转向L2解决方案发展的启发,我们提出了第一个基于FHE的Rollup架构。我们认为,FHE对于明文计算Rollup是一个必要的解决方案,尽管在FHE背景下,计算开销要高出几个数量级。在Rollup架构中,智能合约执行(验证区块的繁重部分)与验证执行和达成共识是分开的。这确保只有单个节点(或少量节点)实际上在执行繁重的计算工作,而不会降低安全性。此外,该节点可以根据需要垂直(和水平)扩展,包括利用更昂贵的专用硬件(GPU、ASIC)。后者在基于ZK的Rollup中很常见 ,与FHE一样,它也利用计算密集型密码学,并且可以以与 FHE 计算大致相同的方式利用。
然而,在我们的设计中,我们采用乐观Rollup方法而不是zk-rollup 方法,这使我们能够避免由最先进的可验证FHE技术带来的数量级损失。事实上,我们的框架可以被视为解决同样问题的加密经济解决方案。
1.1 贡献
在本文中,我们做出了以下主要贡献:
推出Fhenix,第一个L2机密智能合约平台,可实现更高的效率和可扩展性。
我们通过概念验证实施证明,可以在以太坊之上构建乐观FHE rollup,而无需对基础层进行任何更改。虽然我们的工作超出了以太坊和 EVM 链的范围,但表明这在今天的以太坊上是可能的,这意味着最常用的智能合约生态系统可以通过机密智能合约来增强。
在区块链背景之外,我们的解决方案可以被视为解决可验证FHE问题的更有效(加密经济)解决方案。
1.2 相关工作
我们的工作建立在现有的机密智能合约平台研发机构的基础上。与所有其他工作不同,据我们所知,我们是第一个描述完全且原生作为L2运行的解决方案。更具体地说,其他机密智能合约平台通常因其使用的隐私保护技术的种类而有所不同:
• 基于可信执行环境(TEE)。目前,生产中唯一的机密智能合约网络使用的是TEE(或安全飞地secure enclaves)。这些网络通过允许用户使用安全飞地(secure enclaves)内保存的密钥来加密其交易来模拟安全计算。然后,交易在安全飞地(secure enclaves)内被解密并执行,只要我们可以信任 TEE 的安全性,就可以确保机密性。虽然 TEE 是迄今为止最有效的解决方案,但它们容易受到旁道攻击和其他漏洞的影响。
• 基于安全多方计算(MPC)。由于我们的工作依赖于 Threshold FHE,因此我们与这些工作共享类似的威胁模型。然而,出于演示的目的,我们将它们与基于FHE的解决方案分开,因为它们通常依赖于线性密钥共享和乱码电路技术(garbled circuits techniques)。与我们的工作相比,这些技术的主要缺点是MPC协议需要传输与电路大小成比例的数据才能对其进行评估。在基于密钥共享的MPC情况下,所有参与方在评估乘法门时还需要顺序地与所有其他参与方进行通信。在公链背景下,这是不切实际的,因为延迟非常高并且带宽有限。 此外,由于这些系统的每个合约执行都需要多个交互节点,因此它们不适合我们提议的Rollup架构。
• 基于ZK。不同的工作考虑了使用不同 ZK 方案的机密智能合约。然而,由于 ZK 技术更适合可验证计算,因此它们在机密智能合约中的效用受到限制。为了克服这个问题,Hawk建议设立一个数据管理器——一个链外机构,其任务是收集不同客户的输入,并被信任可以查看每个人的数据。或者,其他平台对开发人员施加限制。
• 基于FHE。在过去几年中,由于FHE性能的显著改进,基于 HE 和 FHE 的解决方案开始出现。这些平台与我们的工作最接近,但它们都没有采用Rollup架构,这限制了它们在实践中的可扩展性。其中一些工作像我们一样采用阈值FHE结构,而其他工作允许有限的功能,但没有共享的全局加密密钥对。
二、基础部分
2.1 Rollups
Rollups是一种扩展解决方案,旨在缓解主 L1 (尤其是以太坊)的拥塞。随着以太坊用户群的不断增长,对扩展解决方案的需求变得至关重要。可扩展性的主要目标是在不影响去中心化或安全性的情况下提高交易速度和吞吐量。Rollup在基础层之外执行交易,发回状态更新以及正确执行的证明。最终,L1(在我们的例子中是以太坊)就这些状态更新达成共识,但它不需要在基础层上重新执行交易。换句话说,L2 Rollup 上的交易受到以太坊固有安全性的保护。Rollup 有两种主要类型,其不同之处在于证明的创建和验证方式:
• 乐观Rollup。其假设交易除非受到质疑,否则都是有效的。他们将计算移至链外,但将交易数据发布到以太坊,允许任何人在链外重新运行交易并自行验证执行是否正确。如果任何验证者检测到恶意行为,他们可以在链上提交欺诈证明,在这种情况下,L1 充当最终仲裁者。因此,乐观Rollup需要一个争议期(通常为几天)。
• ZK Rollup。这些Rollup类似地在链外执行合约,并在发送状态更新时提交有效性证明。有效性证明是使用称为(简洁)ZK 证明的先进加密技术构建的。它们可以直接在链上进行有效验证,无需发布完整的交易数据或存在争议期。
Optimistic和 ZK Rollups本质上有不同的权衡。乐观Rollup会受到争议期延迟的影响,从而导致最终结果更长。它们还需要将交易本身发布到链上,这抵消了一些可扩展性优势。
另一方面,ZK Rollups 需要大量的计算能力(和时间)来生成证明,尤其是当你尝试原生EVM 时。一个相关的缺点是这些Rollup的构建要复杂得多,从而导致大量代码。因此,zkEVM 出现严重漏洞的可能性要高得多,至少在它们经过足够时间的战斗测试之前是这样。
2.1.1乐观Rollup详细解读
Optimistic Rollups 将多个链下交易捆绑在一起提交到 L1 链上,降低用户的成本。他们被称为“乐观”,因为他们假设交易是有效的,除非另有证明其是欺诈的。如果交易受到质疑,则会计算欺诈证明。如果证实存在欺诈行为,将受到处罚。如今,乐观Rollup在以太坊上运行,由基于以太坊的智能合约管理。他们在链外处理交易,但将数据批次发布到链上Rollup合约。以太坊确保Rollup计算的正确性并处理数据可用性,使Rollup比独立的链外解决方案或侧链更安全。它们还在两层之间创建了固有的经济安全一致性,因为 L2 在支付 L1 层产生的费用的同时获得安全性。
从架构角度来看,Optimistic Rollup 包含以下内容:
交易执行。用户将交易发送给运营商或验证者,他们将交易聚合并压缩到 L1。
提交给L1。 运营商捆绑交易并使用 calldata 将它们发送到 L1。
状态承诺。Rollup 的状态表示为 Merkle 树。运营商提交新旧状态根,确保链的完整性。
欺诈证明和争议。这些允许任何人质疑交易的有效性。如果挑战有效(由 L1 仲裁),则欺诈方将受到惩罚。
欺诈证明在乐观Rollup中发挥着至关重要的作用,它们是我们确保Rollup发布正确状态更新的根本。即使面对试图延迟或篡改交易的恶意节点,只要有一个诚实的节点观察状态更新并检查它们是否正确,链的完整性就会得到保留。在以太坊上构建的 Rollups 背景下,因为实际数据发布到以太坊上,世界上任何人都可以充当验证者。一旦诚实的验证者检测到不正确的状态更新(例如,通过包含被篡改的交易),它就可以提交争议,从而启动防欺诈游戏:多轮交互协议。在这里,断言者(产生状态更新的节点)和挑战者(发出争议的验证者)遵循由 L1 验证者合约监督的协议来确定诚实方。该协议递归地进行,每次将计算分成两个相等的部分。挑战者每次选择一个部位进行挑战。这一过程称为二分协议,一直持续到只有一个计算步骤有问题为止。一旦交互协议缩小到单个指令,就轮到 L1 合约通过评估指令结果以及断言者和挑战者的声明及其各自的结果来解决争议,以确定哪一个是正确的。
2.2 全同态加密(FHE)
全同态加密 (FHE) 可以对密文进行计算,解密后,这些运算的结果与直接对明文执行的结果相一致。
在实践中,自从Gentry提出原始方案以来,已经开发了几种 FHE 方案,这些方案基于最初的误差学习难度问题(Learning With Errors hardness problem),或相关的代数结构,例如其环变体。我们的实现使用了一种名为TFHE的方案,但由于该方案本身对于构建 FHE Rollup的目的并不重要,因此我们在下面以黑盒方式更一般地描述 FHE。
通用 FHE 方案可以用算法元组 FHE = (Gen, Enc, Dec, Eval) 表示,如下所示:
• Gen(1k)。给定安全参数 1k ,算法输出一对密钥 (pk, sk) ,其中 pk是公共加密密钥,sk是秘密解密密钥。定义明文域P、随机性域R、密文域C,以及允许的函数集F。
• Enc(pk,m;r)。给定公钥pk、消息m∈ P 和随机性r ∈ R,加密算法生成密文c ∈ C ,使得
? = Enc?? (?;?)。
• Dec(??, ?).。使用密钥??和密文 ?,解密算法检索原始明文消息
? = Dec?? (?)。
• Eval(??, ? , {?? } ? ?=1 )。给定公钥??、函数? ∈ F和一组密文{?? } ? ?=1 ,该算法生成密文? ′ ∈ C,使得:
Dec?? (? ′ ) = ? ({Dec?? (??)}? ?=1 )。
这意味着函数?是在加密数据上执行的,其结果被加密为?'。
三、架构
3.1 FHE Rollups:乐观还是基于ZK?
如前所述,ZK Rollups 在证明方面本质上较慢,但这为验证方面提供了好处。在 FHE 的背景下考虑 ZK 时,这个问题变得更加复杂,因为我们现在基本上将两种重型加密技术结合在一起。虽然越来越多的工作试图解决这一研究空白,但目前提出的解决方案速度要慢几个数量级。因此,对于加密域来说,使用基于乐观的方法成为更自然的选择。
3.2 设计概述和实现细节
我们的平台在构建时考虑到了模块化。它包括 Rollup 的典型组件,包括排序器、证明器和 DA 层,同时交织支持 FHE Rollup 所需的新组件和特定组件。图 4 说明了总体设计。我们在下面详细介绍了新的 FHE rollup 特定组件。
3.3 fheOS
FHE核心逻辑位于我们的 fheOS 库中。它是一个预编译常见加密操作码的加密计算库,例如比较两个数字以及进行加法和乘法等算术运算。它使网络上运行的智能合约能够在合约中使用 FHE 原语。这意味着在 Fhenix 上运行(或使用)的 dApp 将能够将加密数据集成到其智能合约逻辑中。开发人员可以选择决定哪些内容将被加密,哪些内容将保留明文。fheOS 是 Zama 的 tfhe-rs 3 FHE 库的另一个 EVM 友好包装器,类似于 fhEVM 。出于实现目的和模块化,我们选择设计自己的版本。
fheOS库是Fhenix节点的核心引擎;利用加密功能的智能合约将调用 fheOS 预编译来执行常见的 FHE 操作,并且 fheOS 本身将负责Rollup和阈值服务网络(TSN,请参阅第 4 节)之间的通信和身份验证,以处理解密和重新加密请求,同时证明解密请求是合法的。
fheOS库旨在作为扩展注入到任何现有的 EVM 中,这意味着它完全兼容 EVM,从而保留所有现有的 EVM 功能,同时提高开发人员探索新用例的能力。
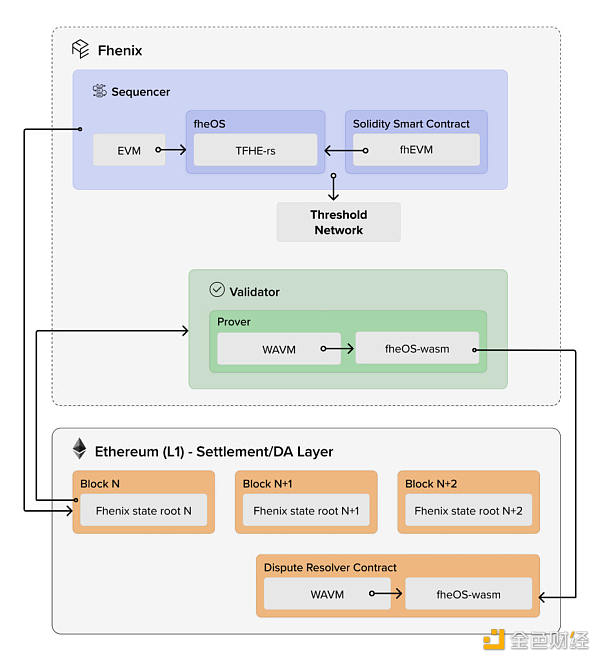
图 1. FHE Rollup 架构概述
3.4 go-tfhe
当我们试图扩展以太坊 goethereum (geth)(他们用 Go 编写的主要客户端)的功能时,我们遇到了一个挑战:核心 FHE 数学运算库 tfhe-rs 是用 Rust 编写的,需要通过外部函数接口(FFI)进行通信。为了解决这个问题,我们开发了 go-fhe,其中包括:
1.基于Go的API。该组件提供了使用 Go 执行 FHE 数学运算的所有必要接口。它是熟悉 Go 的区块链开发人员的主要交互点。
2. TFHE.rs 的Rust包装。我们创建了一个专门的包装器,用于调整 TFHE.rs 库函数以适应区块链应用程序。
3. Go API和Rust Wrapper之间的FFI集成。为了桥接这两种语言,我们的界面采用了 cgo 和 extern“C”机制。这有利于 Golang 和 Rust 之间的绑定,对齐函数调用、类型和命名约定。
一般来说,go-tfhe 充当 tfhe-rs 和区块链应用程序之间的模块化可扩展轻量级桥梁。
四、阈值服务网络(TSN)
我们设计中的一个关键组件是阈值服务网络(TSN)。该网络与 L1 或其他Rollup组件分开,并发挥多个关键作用。特别是,该网络被集体委托给秘密共享的网络密钥[??],可以用于阈值解密。我们当前的实现利用了它,它使用 Shamir 秘密共享将 ?? 分割为 ? 份,其中需要 ? + 1 份来重建。实际上,每个位都是单独共享的,但出于本文的目的,我们将忽略这种区别。
4.1 阈值解密和重新加密
有时,网络需要解密某些结果,或者将它们重新加密给指定用户。TSN 负责来自Rollup的任何此类请求,并且可以使用 阈值解密协议来容纳它。
为了说明为什么需要这样做,请考虑以下两个示例。首先,想象一下部署在 rollup 上的私密投票合约。当用户投票给某个候选人时,他们会对自己的选票进行加密,合约会统计这些选票(全部加密)。在某个时间点,合约中的功能应该能够解密计数并宣布获胜者。该请求被路由到 TSN,TSN 对其进行解密并返回结果以存储在合约的状态中。此流程如图 2 所示 ,Solidity 合约代码片段如图 3 所示。
一个类似的例子是拥有 NFT 的用户,其中的私密元数据只有他们自己才能看到。此类元数据存储在网络密钥下的合约状态中。当用户尝试访问该信息时,合约应该对其进行阈值重新加密,以便只有指定的用户才能解密并访问底层数据。
4.2 秘密共享数据的证明
在某些情况下,我们也许能够利用 TSN 来协助证明有关加密数据的重要陈述。例如,众所周知的事实是,密文需要格式正确,否则尝试解密格式错误的密文可能会泄露有关密钥的信息。同样,在这样的多用户系统中,我们需要确保用户不会(例如)发送他们未加密的密文,并要求 TSN 为他们解密。出于这些原因,每当用户提交加密输入时,我们都需要确保它已被正确加密并且用户知道底层的明文。
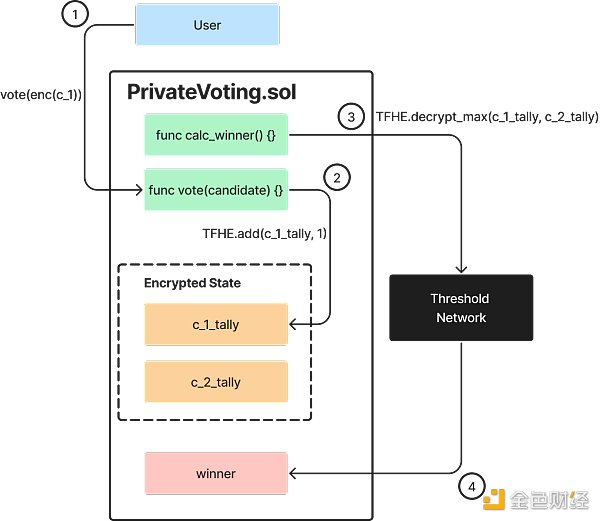
图 2. Fhenix上解密FHE加密数据的智能合约请求
目前,基于 FHE 密文的最先进的零知识知识证明(ZKPoK)仍然相对昂贵,并且会给每笔交易增加大量的开销。一种替代方案是让客户端首先使用可验证的秘密共享协议 (VSS) 将其秘密输入秘密共享到 TSN。在确认输入已正确秘密共享后,网络可以例如通过以下简化的协议草图联合加密输入。
• 协议阈值加密。给定共享用户消息 [?] 和预处理的随机元组 ([?], ????? (?)),各方输出 FHE 密文 ?? := ????? (?)。
• 服务器与客户端运行VSS 协议,接收并验证[?] 的共享。
• 服务器使用主动安全的 MPC 协议联合重建 ? := ????( [?] − [?])
• 输出?? := ????? (?) + ????? (?)。
* 请注意,由于??是安全顺序协议结果的公共值,因此各方可以就其达成共识以确保正确性。
4.3 随机信标
智能合约的一个独特的必要功能是产生随机性。智能合约本质上是确定性的,因此它们需要外部随机性来源来启用非确定性功能。

图 3. Solidity中的FHE投票合约示例
需要此类功能的用例示例包括链上游戏(例如扑克、赌场)、NFT 铸币等。
存在许多分布式抛硬币协议。非常适合我们的案例的一个例子是基于可验证随机函数(VRF)的例子。
4.4 安全洗牌
在许多情况下,我们需要一个专门用于对输入向量进行洗牌的功能。许多隐私保护计算技术,包括那些利用 FHE 的计算技术,都可以从高效的安全洗牌原语中受益。洗牌发挥作用的例子不胜枚举。一个简单的例子是扑克游戏——安全、私密地洗牌至关重要。
更重要的是,安全洗牌是 Oblivious RAM (ORAM) 的关键构建块,这些方案不仅确保内存被加密,而且确保对内存的所有访问都是私密的。使用 ORAM 可以成为构建更高效的 fhEVM 的构建块,该 fhEVM 允许 直接在程序上运行 FHE 计算,而无需首先将它们展开到电路中。其他应用程序,例如构建私密搜索引擎,或在基于帐户的模型中构建真正的匿名代币,需要某种形式的ORAM。
4.5 安全性
需要注意的是,整个系统底层的机密性保障与 TSN 的信任假设密切相关。与保持阈值解密密钥安全、正确解密/重新加密密文等相关的任何事务均由 TSN 负责。
目前,15提出的最先进的协议要求 TSN 最多有 ? < ? 3 个恶意损坏,才能实现快速而稳健的协议,或者 ? < ? 2(如果我们愿意通过中止来满足安全性) 。
4.5.1 拟议的改进(以及开放的未来研究)。我们提出了几个关于 TSN 及其当前阈值解密协议的开放研究领域。我们邀请社区与我们一起推进这些感兴趣的主题:
• 支持不诚实多数的主动安全阈值解密协议
• 作弊者识别——对于支持最多 ? < ? 2 个腐败的协议(或任何不诚实的多数协议),我们应该能够识别作弊方(无论是破坏协议的一方,还是中止协议的一方)。如果没有它,就无法防止对 TSN 的拒绝服务攻击。
• 通过抽样提供许多验证器(>1000)——目前该方案对于许多验证器的扩展性不够好。对于限制为 ? < ? 3 的情况尤其如此,其计算复杂度随着 (?, ?) 呈指数级增加。解决这个问题的一个方法是集中精力为每个时期抽取一个小委员会 [20, 49]。
• 共享轮换和恢复。许多这样的方案已经存在于文献中。
五、欺诈证明
Optimistic Rollups 的关键在于其欺诈证明机制。但我们如何适应该机制,特别是以太坊的 EVM,以与在加密数据上执行 FHE 电路的智能合约配合使用?
首先,观察到 FHE 与 MPC 等其他加密计算技术不同,它本身允许任何人验证计算是否正确完成,而不会破坏隐私保证。这是因为持有加密输入和输出的对手对底层加密数据一无所知(如果不是这种情况,那么加密方案在语义上将不安全)。
这使得验证 FHE 计算与乐观Rollup的思想兼容,至少在理论上是这样。如前所述,乐观Rollup基于在 L1(或其他一些数据可用性服务)上发布完整的交易数据以及输出。在这种情况下,两者都被加密。就像明文数据一样,任何链下验证者都可以获取加密的交易数据,重新执行交易,并确保它们收到相同的加密输出。如果情况并非如此,那么诚实的验证者可以提交争议并开始与 L1 的仲裁过程。
然而,整个欺诈证明机制植根于 L1 明确确定发布状态更新的 L2 节点或有争议的验证者(即挑战者)是否作弊的能力。为此,L1 需要能够运行底层计算的单个计算步骤。由于我们对以太坊作为 L1 感兴趣,这就提出了一个问题:以太坊或任何传统的 EVM 链如何在没有对 FHE 操作的固有支持的情况下验证 FHE 原语的执行?
答案就在 Arbitrum 的 Nitro 欺诈prover证明者中,我们根据需要重新调整了它的用途,允许我们将所有 FHE 逻辑编译到 WebAssembly,并在 WASM runtime (WAVM) 中执行整个证明轮,在以太坊上链上,而不是原生EVM。由于底层 FHE 代码也可以编译为 WASM,因此不需要对 L1 本身进行任何更改。
为了解决性能问题,可以合理地假设,如果 FHE 计算本质上是密集型的,那么在 EVM 之上的 WASM runtime中模拟它们可能会导致严重的性能损失。虽然这是一个合理的担忧,但重要的是要记住,启动这些计算仅在争议场景中是强制性的,并且在有足够争议窗口的情况下,实时速度并不是绝对必要的。考虑到标准做法为此分配了大约 7 天的时间,我们估计这对于解决任何此类争议来说已经足够了。然而,我们没有通过经验验证这一假设,我们注意到,将来验证很重要。
5.1 实施细节
在开发概念验证 FHE 欺诈证明者的过程中,我们必须克服几个障碍,为了完整起见,我们在此予以说明。
首先,为了将 go-tfhe 作为欺诈证明机制的一部分运行,有必要调整代码以在 WebAssembly (WASM) 中执行。鉴于我们对用 Rust 编写的 FHE 代码的依赖,而大部分区块链代码传统上都是用 Golang 编写的,因此我们在原生编译为统一的 WASM 模块时面临着挑战——Rust 和 Golang 之间的默认绑定使用 cgo,与 WASM 不兼容。为了解决这个问题,我们在 WASM 中绑定使用主线Golang 编译器的外部函数指令,在Golang 和 Rust 之间架起桥梁,创建一个专用 Rust 文件作为主要 WASM 构建目标,最终使用 wasm-merge 将两者链接起来以获得内聚的 .wasm 输出。
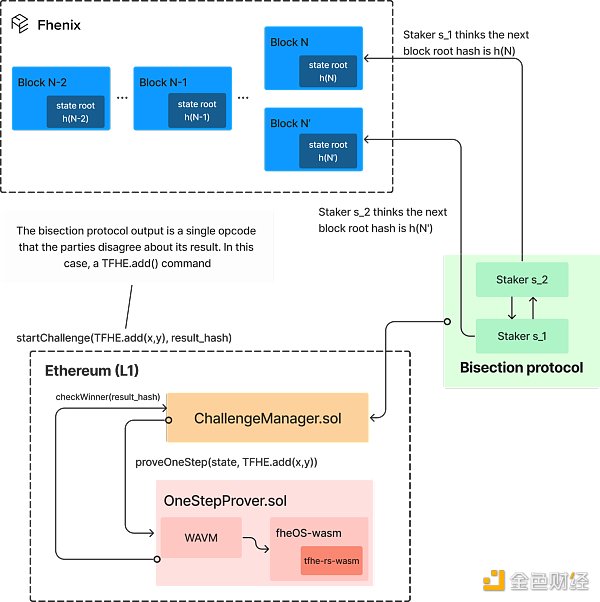
图 4. FHE指令的防欺诈引擎
此外,我们还必须修改 tfhe-rs。在撰写本文时,tfhe-rs 仅支持在浏览器中编译和执行 WASM。在我们的例子中——在区块链之上运行的智能合约——可用的接口与浏览器的接口不同。值得注意的是,某些 API 调用(例如访问操作系统功能或多线程)无法访问。为了使 TFHE.rs 与智能合约上下文兼容,进行了两项主要修改:
1. 禁用多线程。鉴于大多数智能合约不支持多线程或并发,因此代码被调整为以单线程和确定性方式运行。
2. 自定义随机数提供商集成。tfhe.rs 的初始版本依赖于预定义的随机数提供程序或播种程序。唯一可用的播种程序取决于操作系统生成随机数的能力。我们引入了由Lib用户管理的自定义播种程序。该播种程序接收输入种子并将其传递到基于 ChaCha20 的种子伪随机数生成器 (PRNG) 提供程序。此修改消除了 FHE 实现中对非确定性随机数的需求,通过使用来自区块链数据和状态的一致输入复制计算来促进外部验证。
我们注意到,根据在此上下文中运行的 tfhe-rs 基准测试,使用 wasmer/cranelift 时性能会出现数量级下降,而使用 wasmer/llvm 进行添加操作时性能会下降 8 倍(在 i9-13900K、128 GB RAM、wasmer 4.0上测试) )。我们注意到 Arbitrum 欺诈证明引擎使用软件浮点,这应该会进一步影响性能,但在撰写本文时我们尚未完成基准测试。
六、结论
在本文中,我们展示了第一个提出的FHE Rollup构造,这是一种为以太坊和其他EVM链增加机密性的新颖解决方案。我们的方法利用FHE的力量来实现加密的EVM计算,彻底改变了交易的执行方式和链上处理机密数据的方式。与最近的工作不同,我们的方法使用L2 Rollup结构来避免在所有节点上复制FHE计算的成本,从而产生更高效和实用的解决方案。
我们的方法侧重于以太坊和EVM,但作为支持可验证 FHE 的系统也具有独立价值。此外,我们还提出了我们提出的 FHE rollup 系统的架构,包括其组件和层,并提出并实施了防欺诈解决方案的概念验证,该解决方案不需要对以太坊进行任何更改。我们的工作有助于开发新一波以隐私为中心的去中心化应用程序,增强用户信心,扩大潜在用例,并提高以太坊网络的整体安全性和实用性。







