Bitwise和VettaFi调查:仅39%金融人士认为年内推出现货比特币ETF
作者:Jon Gulson,Bitcoin Magazine;编译:松雪,金色财经
“我认为经济学有点像会计 —— 你知道的,它并不涉及任何道德。你可以研究福利经济学,尝试考虑一些人类价值观,或者你可以研究各种变体。” —— 约翰·F·纳什 Jr.,斯克兰顿大学,2011年11月。
这段引自约翰·福布斯·纳什·Jr.的语录——来自他在“理想货币和储蓄与节俭动机”上的一次演讲,此次演讲距离他第一篇博弈论论文《讨价还价问题》(1950年)发表已有61年。
《讨价还价问题》之所以重要,是因为它被认为是社会科学中首次引入公理方法的例子之一。纳什将《讨价还价问题》作为一个对古典经济问题的新处理 —— 将其视为一个非零和、两人博弈,在这个博弈中他做出了一些一般性假设和“某些理想化”,以便为博弈找到值。
从《讨价还价问题》到纳什后来关于理想货币的研究的基因谱系被确立,而在《讨价还价问题》中,纳什对货币的效用进行了评论:
“当讨价还价者有一个共同的交换媒介时,问题可能呈现出特别简单的形式。在许多情况下,商品的货币等价物将作为一个令人满意的近似效用函数。” 约翰·F·纳什 Jr.,《讨价还价问题》(1950)。
纳什的讨价还价探讨在金融交易或合同中,如何在参与者之间公平地分割1美元,每一方都有一系列的兴趣和偏好,并且必须达成协议,否则双方都将一无所得。为纳什交易引入的公理随后定义了一个唯一的解决方案。
纳什均衡与纳什讨价还价
在《The Essential John Nash》(2007)中,哈罗德·库恩描述了纳什随后的《Non-Cooperative Games》(1950)论文,以及后来被称为Nash均衡的理论,他称之为对Brouwer不动点定理的“笨拙,但完全独创的应用”。然而,正是纳什的均衡概念通过经济科学诺贝尔奖赋予他公众关注。后来,纳什的生平被改编成了好莱坞电影《美丽心灵》。
在《Non-Cooperative Games》中,纳什的理论基于“联盟的缺席,即假设每个参与者都是独立行动的,没有与任何其他人的合作或沟通”。在亚当·柯蒂斯(Adam Curtis)的电视纪录片《陷阱》(2007)中,纳什将他的均衡理论描述为社会调整:
“……所使用的这种均衡是,我所做的完全与你所做的相适应,而你所做的或任何其他人所做的也完全适应我所做的或所有其他人所做的。他们正在寻求独立的优化,就像扑克牌玩家一样。” 约翰·F·纳什 Jr.,《陷阱》(2007, 亚当·柯蒂斯),《F*ck You, Buddy》。
纳什均衡和纳什讨价还价的区别在于,公理讨价还价(或达成纳什讨价还价)不假定均衡。相反,它陈述了解决方案的期望性质。纳什讨价还价被认为是合作博弈论,因为它具有非零和的特性和合同的存在。纳什在《Two-Person Cooperative Games》(1953)中扩展了对《讨价还价问题》的公理处理,在这一过程中引入了一种威胁方法,其中有一名裁判来执行合同 —— 在这个过程中,将“策略”视为不具有特殊品质,而更关注确定博弈的形式表示。
理想货币和渐近理想货币
在世纪之交,约翰·纳什开始撰写并讲授一个不断演变的名为理想货币的论文。随着多年的发展,这个理论经历了不同的迭代,但纳什定义它为内在免受通货膨胀或通货膨胀性堕落的货币。纳什对经济学家或个人凯恩斯并不是那么批判,而是对所谓的凯恩斯主义心理学的批评;纳什认为这是一种持续通货膨胀和货币贬值的权谋计划。纳什认为,如果中央银行要以通货膨胀为目标,他们应该将“所谓的通货膨胀”定为零率:
“真正令人尊敬的是,通货膨胀不应该有任意或反复无常的模式,但如何定义一种合适和理想的货币价值稳定形式呢?” 约翰·F·纳什 Jr.,《理想货币和渐近理想货币》(2010)。
在《理想货币》中,纳什回到了他在初期博弈论中首次建立的公理方法。因此,理想货币对凯恩斯宏观经济学提出了批评:
“因此,我认为凯恩斯派的宏观经济学可与使用不足的公理集进行的数学领域的科学研究相媲美。” 约翰·F·纳什 Jr.,《理想货币和渐近理想货币》(2008)。
纳什定义了缺失的公理:
“缺失的公理就是一个被接受的公理,即由中央当局投放市场的货币应该被处理得以在很长时间内保持稳定的价值。” 约翰·F·纳什 Jr.,《理想货币和渐近理想货币》(2008)。
在2002年的《理想货币》南方杂志版本中,纳什意识到理想货币不能完全免受通货膨胀(或过于“良好”),因为它将在流通中遇到问题,并可能被希望安全存放财富的一方所利用。纳什随后引入了一个稳定而恒定的通货膨胀率(或渐近线),该率可以被添加到借贷合同中。
确实,纳什在合作博弈和微观经济背景下描述了理想货币的目的:
“一个我们在初次思考理想货币时没有考虑到,后来才意识到的概念是,在一个经济社会中使用的货币的比较质量对于合同的精确性至关重要,作为未来合同履行的质量指标。” 约翰·F·纳什 Jr.,《理想货币和渐近理想货币》(2008)。
比特币作为一种公理设计
如果纳什对经济学的看法是它缺乏任何直接的道德观念 —— 价值观、假设、公理、变体或理想化可以被引入以确定一个非零和或确定的博弈,为所有参与者提供福祉 —— 那么值得考虑的是,这些公理是否存在于比特币系统中,鉴于纳什与中本聪一起都对中央管理货币的任意(或不确定)性质提出了批评。
帕累托效率
在比特币的累积供应密度和分布方面,帕累托效率的存在可能是最具示范性的纳什讨价还价公理(见图示):大多数比特币在比特币历史的早期被挖出(大致地遵循帕累托80/20幂律)。
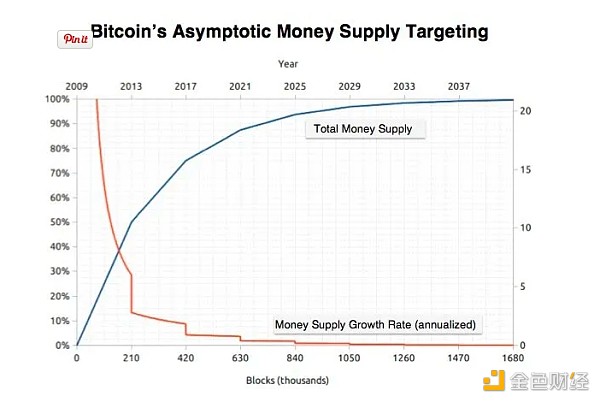
1.尺度不变性
尺度不变性通过难度调整机制而存在,该机制使比特币供应“稳定而恒定”(纳什和中本聪都使用过这个词)。无论比特币变得多么受欢迎或不受欢迎,尺度不变性应该意味着参与者可以形成有关比特币价值的现实期望,而其基本偏好在这方面不应该发生变化。比特币的内部可分割性也意味着在较短或即时时间范围内,一个币的表达价值(无论是美元还是其他货币)不应该有关系 —— 就像室温可以用摄氏度或华氏度表示而不影响实际温度一样。这些差异只在较长期或跨时间的交易中才会变得明显。
调整机制还使比特币的总供应量保持在2100万以下,这是由于系统数据结构的副作用,因此这样设定。
2.对称
纳什的对称性公理存在于比特币网络的匿名和去中心化中,通过在参与核心或主要网络时无需证明第一人称身份,实现了匿名(纳什在《讨价还价问题》中引入的一种说法)。这意味着没有一个中心化或受信任的主体负责铸造比特币,用纳什的话说是一个“大赦者”。与纳什讨价还价相关,如果两个玩家有相同的效用函数,因此是不可区分的,那么它们应该得到相同的数量。阿尔文·罗斯(1977年)总结为玩家的标签无关紧要:“如果切换玩家的标签不会改变讨价还价问题,那么它就不应该改变解决方案。”
3.不相关替代方案的独立性 (IIA)
最后,有纳什最具争议的讨价还价公理:无关替代品的独立性。简单来说,这意味着在两名玩家之间的选举中添加第三方(或非获胜候选人)不应该改变选举的结果(第三方变得无关紧要)。如果点对点是指一个两名玩家的游戏,比特币网络充当第三方仲裁者或裁判员对“游戏”进行操作,该软件设计为一组价值观或公理,那么在比特币的工作证明中可能存在无关替代品的独立性。这涉及到社会群体偏好的背景:工作证明表示它解决了在多数决策中确定代表的问题,并且纳什的讨价还价公理(无论是在《讨价还价问题》还是《两人合作博弈》中)明确解决了决定性游戏中的正式代表问题。
合作特点及效益
一般来说,合作博弈需要具备三个条件:
1.减少参与者,即两名玩家。
2.合同,参与者能够就合理的联合行动计划达成一致,可由法院等外部机构强制执行。
3.参与者能够在可信信息的基础上进行交流和协作,并能够完全访问游戏的结构(例如比特币区块链)。
在非零和游戏和货币偏好方面,约翰·纳什思考了货币如何通过“润滑”促进可转让的效用,并做出了以下观察:
“在博弈论中,通常有‘收益’的概念,如果游戏不仅仅是赢或输(或赢、输或平局的游戏)。游戏可能涉及到同时进行的所有行动,以便用于定义收益的效用度量可以在相关时刻采用任何具有良好可分性和可测性特性的实际货币。” 约翰·F·纳什(John F. Nash Jr.),《理想货币与储蓄和节俭的动机》(2011)。
合作的好处包括减少对调解或纠纷解决的需求,因为合同和协议变得更加可信任;在贸易中减少边境摩擦;非零和结果(双赢的讨价还价或福利经济学);更直观、非正式的决策制定;以及形成联盟的可能性,这正是约翰·纳什最终定义的世界帝国背景。后者使得解决诸如零净排放(或任何其他需要多边协调的问题)的困难问题更加现实。纳什将他的理想货币提议比作老式的主权货币:
“任何版本的理想货币(本质上不受通货膨胀影响的货币)都必然类似于提供用于交易的实用媒体的古典‘君主’或‘领主’。” 约翰·F·纳什(John F. Nash Jr.),《理想货币与储蓄和节俭的动机》(2011)。
2011年,纳什还思考了一个“合同签署”的“游戏”,仿佛理想货币就是这份合同:
“就好像在合同签署者的游戏中还有另一个玩家,而这个玩家就是君主,他以货币的形式提供了合同的表达方式。” 约翰·F·纳什(John F. Nash Jr.),《理想货币与储蓄和节俭的动机》(2011)。







