分析 | 如何判断比特币支撑位和阻力位的位置?
发布方:XBITRUST & Paiclub Capital
作者:苏文杰
我们根据多个交易所的限价指令薄数据构建了一种比特币市场整体情况指标,借此来揭示市场整体深度情况,并采用贝叶斯统计来推断支撑位和阻力位的位置。
交易所的选择参考了BitMEX指数和Deribit的BTC-USD指数获取数据源,采用了Binance、Bitstamp、Bittrex、Coinbase Pro、Gemini、Huobi、Kraken和OKEx交易所的比特币现货数据,并将其挂单量的单位统一为美元,以便比较。
一、聚合后的限价指令薄
下图为2021.2.1 18:03左右时,各交易所聚合后的高于1万美元的挂单情况:
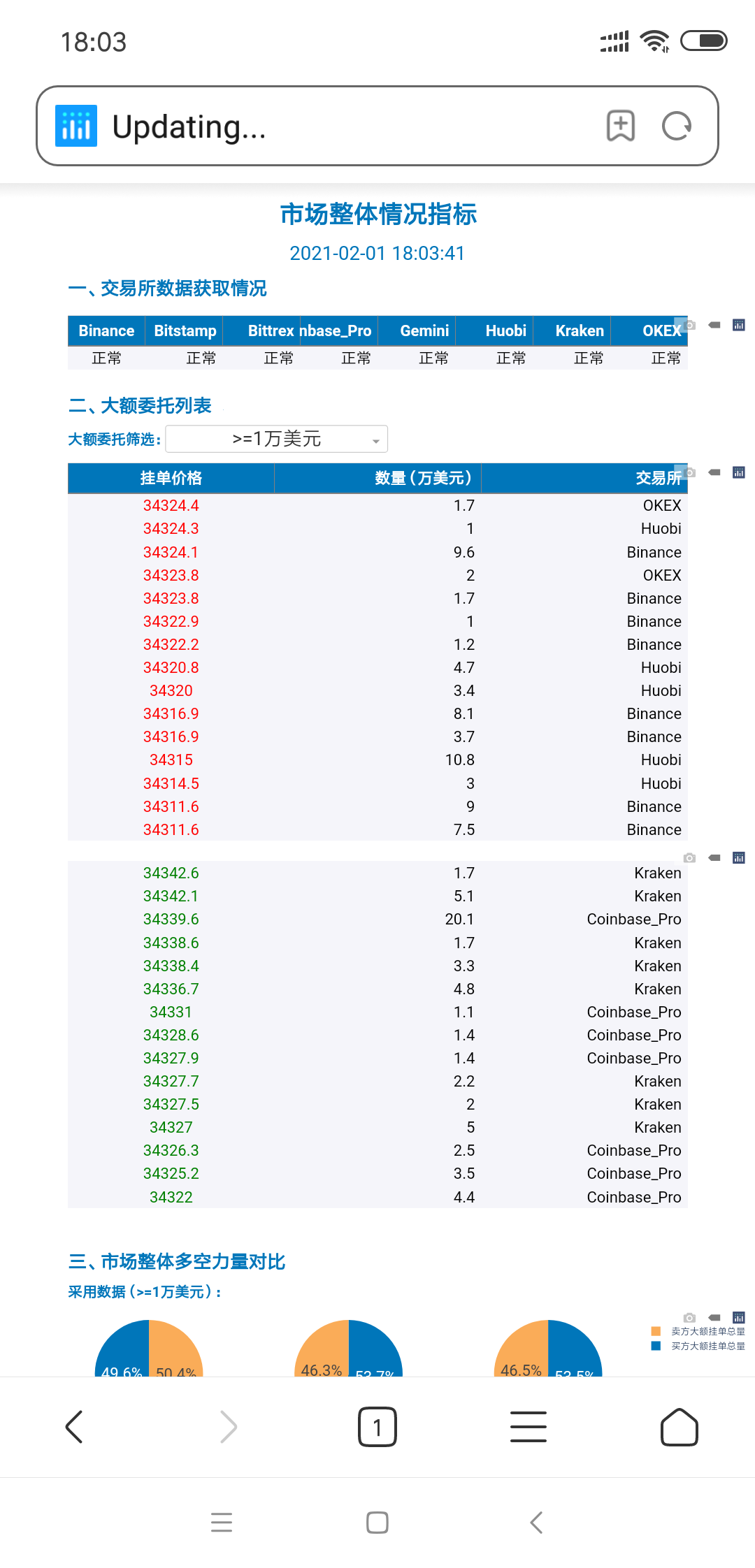
图1 高于1万美元的挂单情况
由上图可知,此刻Kraken和Coinbase Pro的买价高于Binance、Huobi和OKEx的卖价。实际上,有时部分交易所的买价高于其他交易所的卖价的程度较大,这便提供了一定的套利机会。
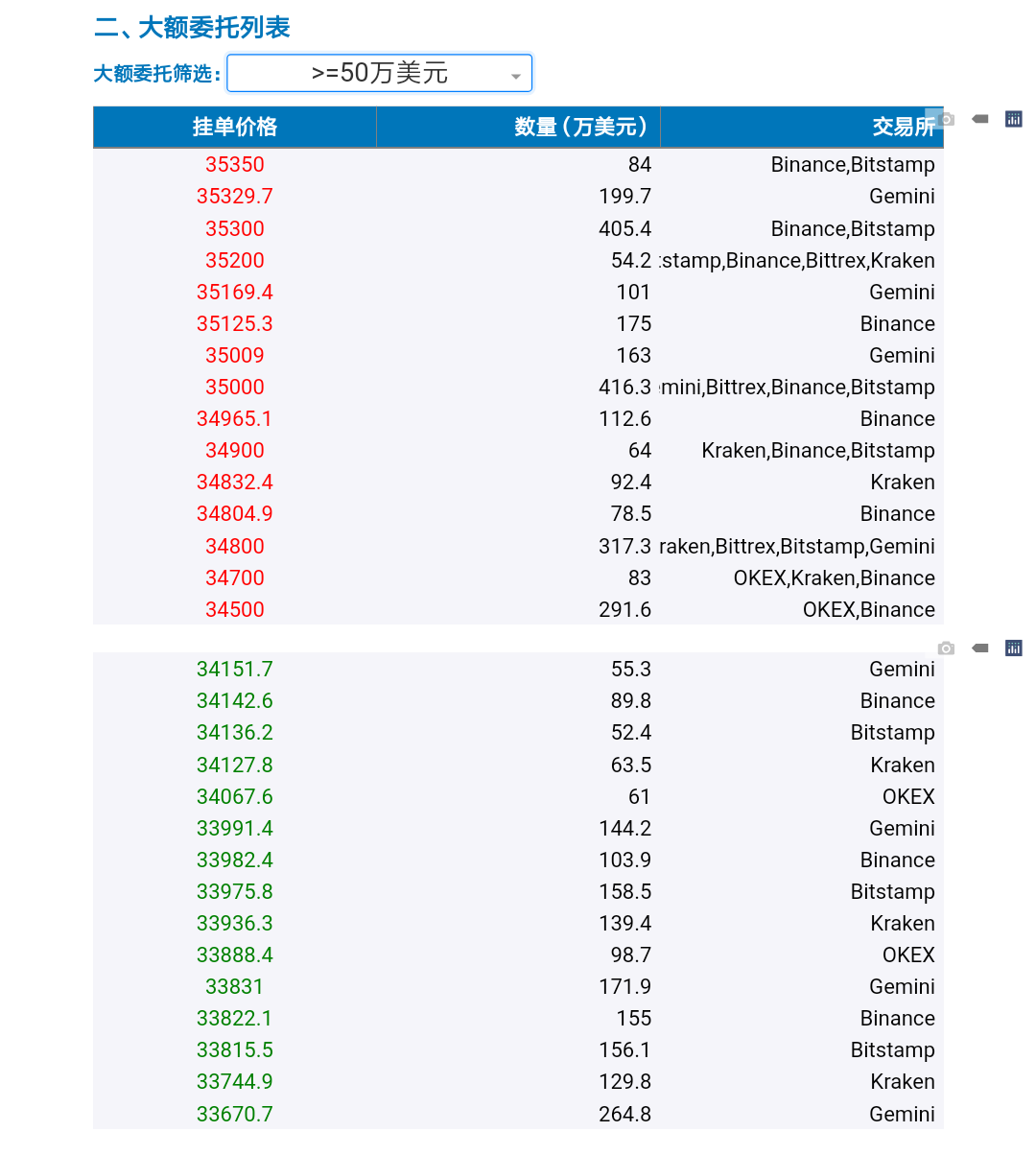
图2 高于50万美元的挂单情况
上图展示了比特币现货市场高于50万美元的挂单情况,不同价位的挂单量是由各个交易所的数据聚合而来的。例如,34700卖价上有价值83万美元的比特币出售,这是由OKEx、Kraken和Binance这3家交易所的挂单所组成的。
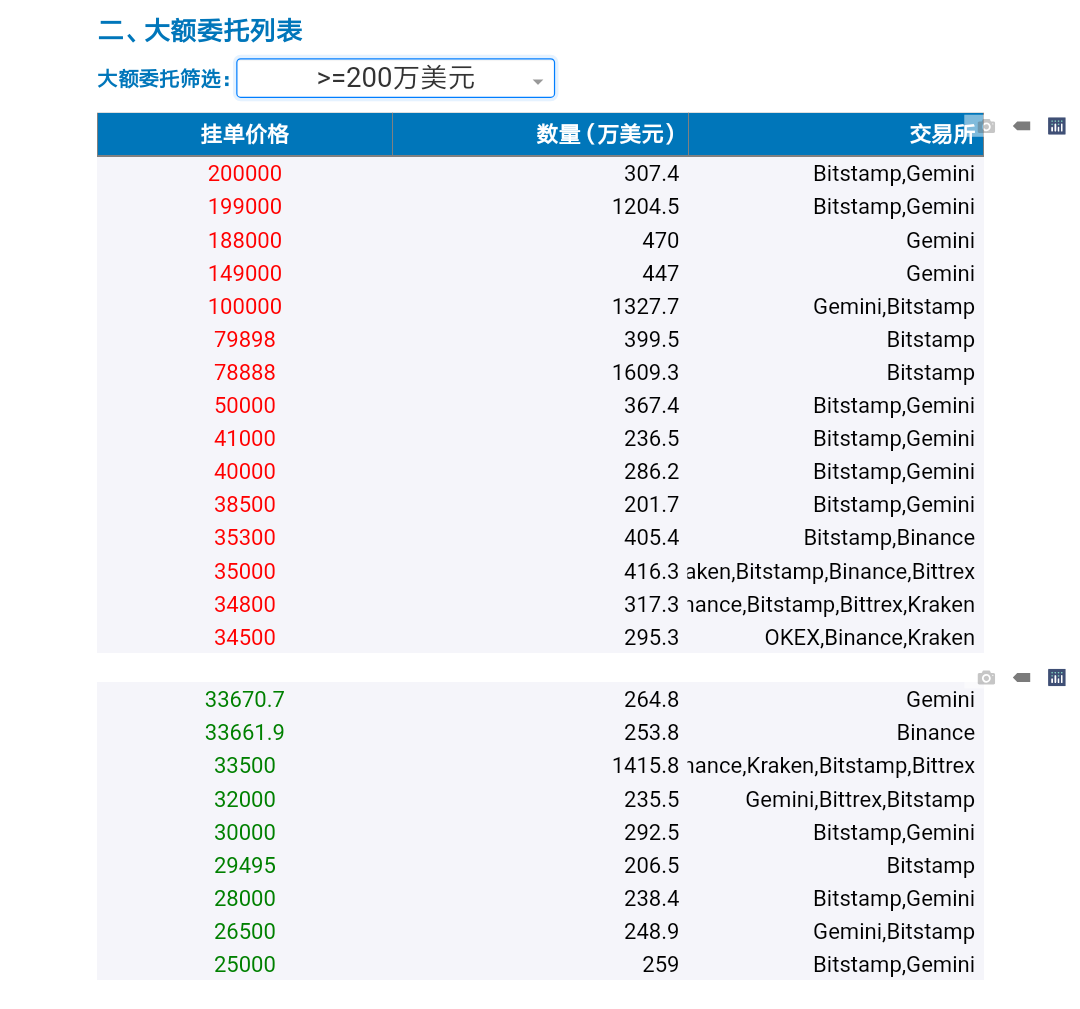
图3 高于200万美元的挂单情况
上图只选择显示高于200万美元的挂单,可见在33500美元至38500美元之间各有一些大额挂单,其金额大致相当,若进一步分析这些挂单的分布情况,我们还能得出更多的结论。

图4 高于500万美元的挂单情况
上图只选择显示高于500万美元的挂单。有意思的是,有部分报价大幅偏离当前价格的卖单长期存在于某些交易所中,而这样的挂单一般不纳入到我们的分析之中。
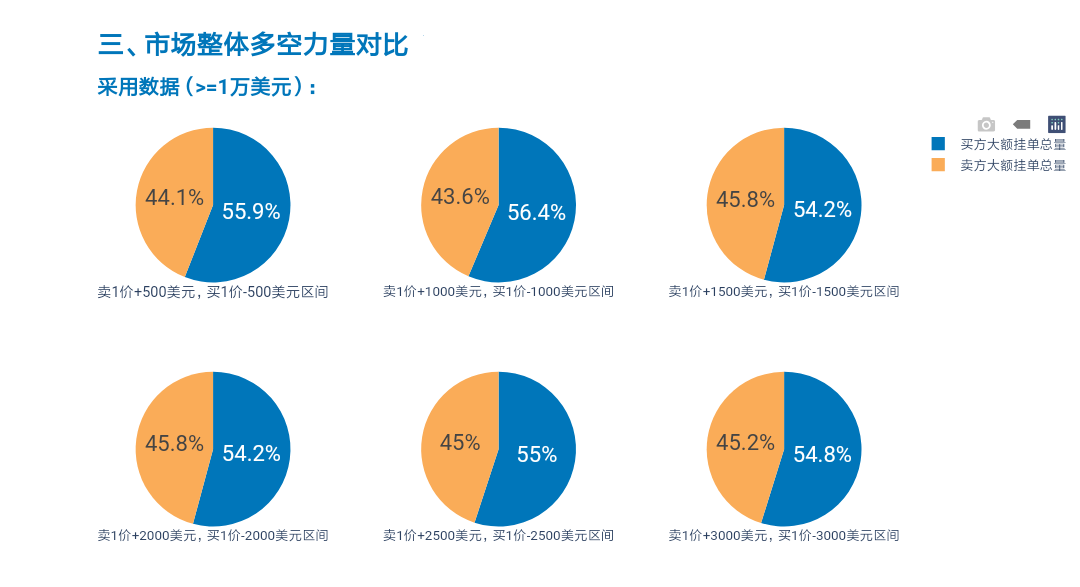
图5 市场整体多空力量对比
上图给出了不同价格区间下,市场整体多空力量对比情况。由此可知,此刻买方的大额挂单总量略大于卖方,不过这样的结论作为指标值也只适合在震荡行情中进行选用。
二、贝叶斯统计在比特币支撑位和阻力位判定中的应用
在交易中,人们一般基于经验来判断某个价位是否是支撑位或阻力位。在限价指令薄中看见各价位的挂单量时,很自然地就瞬间对比出哪些价位的挂单量大于其他价位,且数值有明显的不同之处,属于支撑位或阻力位。
人脑对此的判断迅速准确,但要问起判断依据,其回答通常是“感觉到是这样”,然后就得出了正确结论。若对此进行一番分析,我们可以指出做出这样的判断至少经历了以下4个步骤:(1)人脑对以往的支撑位/阻力位的挂单量有印象,能够以此为经验来考量新的挂单量是否达到相应的量级;(2)人脑对近期的行情表现有印象,清楚市场交易是属于清淡还是火热状态,对心目中支撑位/阻力位的合理挂单量进行了相应的调整;(3)在看见限价指令薄的一瞬间,就能立即锁定几个大额挂单作为支撑位/阻力位的备选项;(4)迅速判断出备选的几个大额挂单在量级上的差异,从而确定支撑位/阻力位。
在量化交易中,我们不可能人工对支撑位/阻力位进行一一标记,只能交给程序来进行相关判断。使用平均值法或移动平均法似乎能简单地解决标记问题,但其适应性和“智能性”还有一定的欠缺。因此,我们使用贝叶斯统计来判定支撑位和阻力位。
在进行正式的介绍之前,先以一个不太严谨的例子来介绍贝叶斯统计:
一个原始人始终在地下洞穴中生活,某天他偶然来到了地面。他不确定太阳是否每天都会升起,于是先按照自己的经验提出假设,然后再进行观测。若他假设太阳每日都会升起,而每天的观测数据也证实了太阳升起这一事件,那么他便可以得出太阳每天都会升起的结论;相反,若他假设太阳不会升起,而每天的观测数据与他的假设不同,基于实验数据推翻了假设,也会得出相同的正确结论——只不过这位原始人为了更有把握,可能较前一种情况观测得更久一些。
这其实就是贝叶斯统计所蕴含的思想——不管假设(先验概率)如何,通过观测数据来修正假设,最终得出符合观测事实的结论(后验概率)。这也类似于人类在科学探索中提出假设,进行实验观测,得出最终结论的方式。可见,从这个意义上来讲,贝叶斯统计与人类的思考和探索方式是具有一致性的。
1、贝叶斯统计方法[1]
统计学中有两个主要的学派,频率学派和贝叶斯学派。他们之间既有共同点, 又有不同点。
基于总体信息和样本信息进行的统计推断被称为经典统计学,它的基本观点是把数据(样本)看成是来自具有一定概率分布的总体,所研究的对象是这个总体,而不局限于数据本身。二十世纪下半叶,经典统计学在工业、农业、医学、经济、管理、军事等领域获得广泛的应用。这些领域中又不断提出新的统计问题,这又促进了经典统计学的发展。随着经典统计学的持续发展和广泛应用,它本身的缺陷也暴露出来。
统计推断中,除了上面提到的总体信息和样本信息外,在周围还存在着第三种信息——先验信息,即在抽样之前有关统计问题的一些信息,主要来源于经验和历史资料,它也可以用于统计推断。
基于总体信息、样本信息和先验信息进行的统计推断称为贝叶斯统计学。它与经典统计学的主要区别在于是否利用先验信息。在使用样本信息上也是有差异的。贝叶斯学派注重已出现的样本观察值,而对尚未发生的样本观察值不予考虑;贝叶斯学派很重视先验信息的收集、挖掘和加工,使它数量化,形成先验分布,参加到统计推断中来,以提高统计推断的质量。忽视先验信息的利用,有时是一种浪费,有时还会导致不合理的结论。
2、贝叶斯公式[2]
在全概率公式的假定下,有
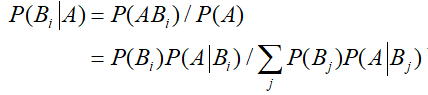
这个公式就叫做贝叶斯公式,是概率论中一个著名的公式。这个公式首先出现在英国学者T·贝叶斯(1702-1761)去世后的1763年的一项著作中。

3、先验分布的确定 [1]
贝叶斯统计中要使用先验信息,而先验信息主要是指经验和历史资料。因此 如何用人们的经验和过去的历史资料确定概率和先验分布是贝叶斯学派要研究 的问题之一。
在经典统计中,概率是用非负性、正则性和可加性三条公理定义的。概率的确定方法主要是两种。一是古典方法(包括几何方法),另一种是频率方法。实际中大量使用的是频率方法,所以经典统计的研究对象是能大量重复的随机现象,不是这类随机现象就不能用频率的方法去确定其有关事件的频率。这无疑就把统计学的应用和研究领域缩小了。譬如,很多经济现象都是不能重复或不能大量重复的随机现象,在这类随机现象中要用频率方法去确定有关事件的概率常常是不可能的或很难实现的。
贝叶斯学派是完全同意概率的公理化定义的,但认为概率也可以用经验确定,这是与人们的实践活动一致的。这就可以使不能重复或不能大量重复的随机现象也可谈及概率。同时也使人们积累的丰富经验得以概括和应用。贝叶斯学派认为一个事件的概率是人们根据经验对该事件发生可能性所给出的个人信念,这样给出的概率称为主观概率。对于先验分布的确定,可以利用先验信息或者边缘密度。而对于没有先验信息的情况下确定先验分布,许多统计学家对这个问题进行了研究,至今已经提出了多种无信息先验分布,例如,贝叶斯假设。
4、似然函数[2]


5、后验分布的计算
(1)贝叶斯公式的密度函数形式

(2)贝叶斯公式的离散形式

上面给出了贝叶斯公式的密度函数形式和离散形式,亦即后验分布的计算公式。而更具有普适性的,进一步包含了不可观测的状态变量和多个参量的后验分布计算公式在这里就不再赘述了。
6、贝叶斯统计在比特币支撑位和阻力位判定中的应用

(1)备选大额挂单数据的保存
我们在数据库中保存初步筛选的大额挂单,取一定的时间间隔,对最新的时间间隔的这些挂单数据进行统计分析。筛选条件和时间间隔的大小是根据特定的模型决定的,这里不做特别的指定。
(2)先验分布
我们的先验分布有三个。
第一个是均匀分布,其随机变量用mu表示,均匀分布的上界和下界分别为上述保存的大额挂单的最大值和最小值,故取其中任意一个数值的概率是相同的。这样,此区间的任意一个数值都有同样的机会被选中,这就在模型中减弱了主观因素的影响。
第二个是半正态分布,其随机变量用sigma表示,其标准差根据特定的模型决定,可根据实际情况调整。采用半正态分布的原因是这些大额挂单都是正数。
第三个是一个均值较小的指数分布,其随机变量用nu表示。这同样是一个很弱的先验。
(3)似然函数
我们用t分布而非正态分布来描述似然函数。t分布的三个参数:均值、尺度(与标准差类似)和自由度分别为mu、sigma和nu。t分布常常用于对呈正态分布的总体的均值进行估计,其峰度比标准正态分布低,尾部比标准正态分布厚。t分布并不像高斯分布那样聚集在均值附近,它希望看到在偏离数据中心的两个方向上都有数据,因此可运用其来解决异常值。在本文的模型中,与正态分布相比,t分布的估计值更鲁棒。
而限于篇幅,我们将不再详细介绍边缘分布。
(4)统计分析
以2021.2.4 19:40为例,我们对本模型并行运行4次,对同一个参数获得4条并行的迹。
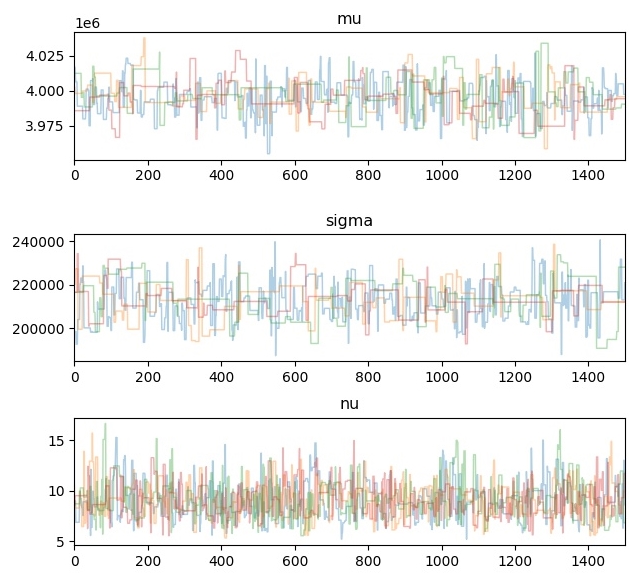
图6 收敛效果
由上图可知,后验分布中的参数mu、sigma和nu均已收敛。我们同时采用Gelman-Rubin检验来判断收敛情况,该检验的思想是比较不同迹之间的差异和迹内部的差异,如果得到的值低于1.1,则可以认为相应的参数已经收敛。经过计算,mu、sigma和nu在此检验下的值分别为1.02、1.02和1.01,故应视为收敛。
我们获得后验分布的参数的贝叶斯估计如下:

图7 后验分布的参数的贝叶斯估计
我们比较关心的是mu的情况。观察第2行,HDI是一个概率,由后验分布观测新数据形成,97%的HDI给出了97%的最可信的值,我们取其为合格支撑位/阻力位应满足的挂单量限制,其数值为401.8万美元。
在此限制下,便可得到合格的支撑位和阻力位:
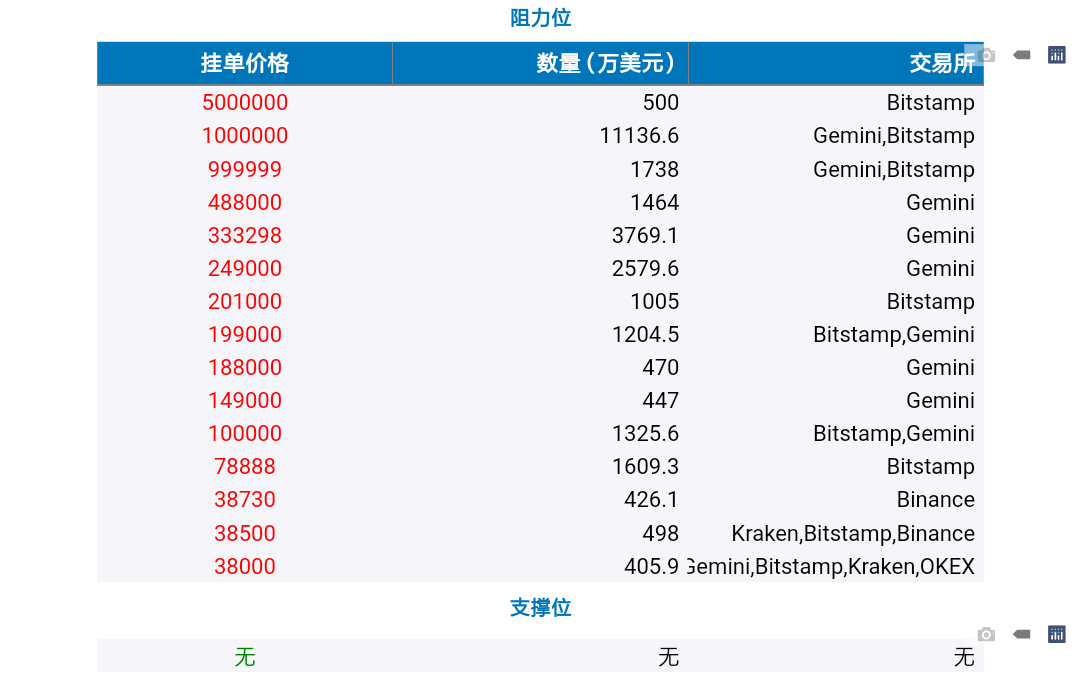
图8 支撑位和阻力位
如上图所示,在此时刻无合格的支撑位,有3个价格分别为38000,38500,38730美元的阻力位。偏离合理价格过大的阻力位不纳入到分析之中。
而根据经验,最近一段时间的支撑位/阻力位的下限随行情的变化在200-800万美元之间变动。由于现货不能像期货一样使用高倍杠杆,在此范围内的挂单量就已经比较巨大了。
三、结论与讨论
本文采用贝叶斯统计对比特币的支撑位和阻力位进行了判定。在此问题的处理上也可采用更为简单的平均值法和移动平均法,但其适应性和“智能性”与本文所用的方法相比会有一定的欠缺;也有更加复杂的方法可对此问题进行讨论,而与之相比本文的模型简单、易于理解、计算便捷,具有一定的优势。
在有条件的情况下,可以尝试采用此法作为量化指标来运行交易程序。需要注意的是,支撑位和阻力位的判定一般在震荡行情的交易中才略有效果,在实际交易中还应结合其他指标一起运行,以便控制风险。
参考文献
[1] 任枫. 非对称双指数跳跃扩散模型的贝叶斯分析. 天津大学硕士学位论文, 2007. 22-24
[2] 陈希孺. 概率论与数理统计. 合肥:中国科学技术大学出版社, 2016. 32-150







