一种安全的 LP 价格的获取方法:以Alpha Finance为例
前言
目前,使用 LP Token 进行抵押借贷的需求越来越大,但是目前市面上并没有一种完善的用于安全获取 LP Token 价格的方法。慢雾安全团队在分析 LP Token 价格的获取方式的过程中关注到了 Alpha Finance 团队的关于安全获取 LP 价格的方法。在仔细阅读后,将相关的思考分享给大家。
LP Token 价格获取分析
目前,常见的 LP Token 价格的获取方式如下:
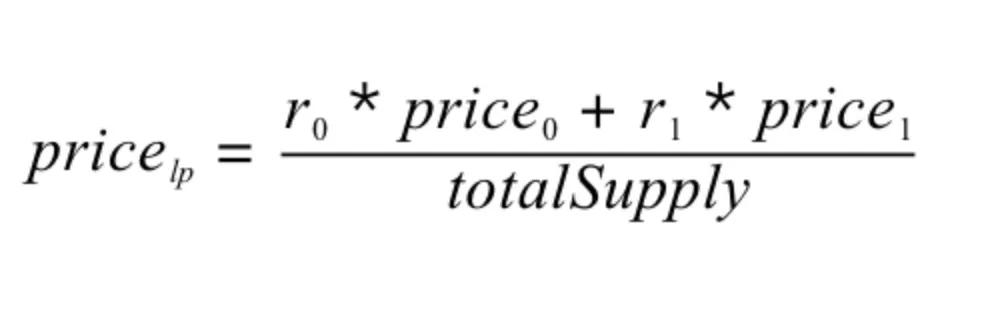
其中,r0,r1 分别代表 Uniswap 交易对中两种代币的存量,price0,price1 分别代表 r0 和 r1 对应代币的价格。上面的公式简单来说就是算出交易对中两种代币的总价值之和,然后除以 LP Token 的总数量,得到了单份 LP 的价值。
这个公式咋一看没什么问题,一般来说,price0 和 price1 都会取 Uniswap 本身提供的延时价格。但是这里存在一个被闪电贷攻击的风险。虽然 price0 和 price1 是不能操控的,但是 r0 和 r1 却是可以操控的。通过操控 r0 和 r1 的值,即可对整个公式进行操控,具体可参考慢雾文章《采用延时喂价还被黑?Warp Finance 被黑详解》
那么有没有办法能获取一种安全的 LP Token 价格,使代币的存量无法被操控呢?Alpha Finance 团队提供了一个思路:

根据 Alpha Finance 的分析,整个过程分为 3 步:
- 第 1 步是通过 Uniswap 的 getReserves 接口获得交易对中对应代币的数量,算出 K
- 第 2 步是获取交易对中每个代币对应的价格,然后算出代币的价格的比例 P
- 第 3 步是通过 K 和 P 之间的关系反推真实的代币存量。
完成以上 3 步后,最终 LP Token 的价格获取公式会变成下面这个样子:

这一波操作下来,好像有点整懵了,但是问题不大,我们来逐个分析。
首先,我们知道,Uniswap 采用的是恒定乘积算法。简单来说就是 x * y = K ,也就是说,交易前后的 K 值是不会变的。在不讨论手续费的情况下,K 值理论上是不会改变的。我们先记住这个前提。然后,获取交易对中每个代币各自的价格,比方说对 USDT 价格。这里以 ETH-BTC 交易对为例,假设 ETH 的价格为 650 USDT,BTC 的价格为 22,000 USDT,那么 ETH/BTC 的价格比值 P 为 0.03。在得到价格的比值 P 之后,直接用第 1 步得到的 K 计算 K/P 和 K*P 就得到了对应交易对的一个正常的数量。下面要对第 3 步,即获取正常的数量这一步进行相应的说明。
公式思路解释
现在开始对上面的第 3 步进行说明,扶稳坐好 :D
像前面说的,恒定乘积的公式为:
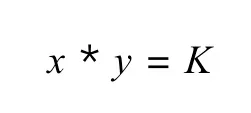
那么其实可以根据 K 来分别算出 x,y。然后根据上一节的第 2 步,我们得到了 x 和 y 的价格的比值 P。由于 Uniswap 本身是根据池中代币的比例来确定对应的价格,所以比值 P 本身就是 x/y 的价格的比值。然后,由于 K = x * y,而 P 是由正确的价格算出的比值,那么,我们其实就可以以这个真实的 K 和 x/y 来反推真实的 x 和 y 。
推算如下:
首先,我们根据 P 和 r0,r1 的比例得出以下公式:
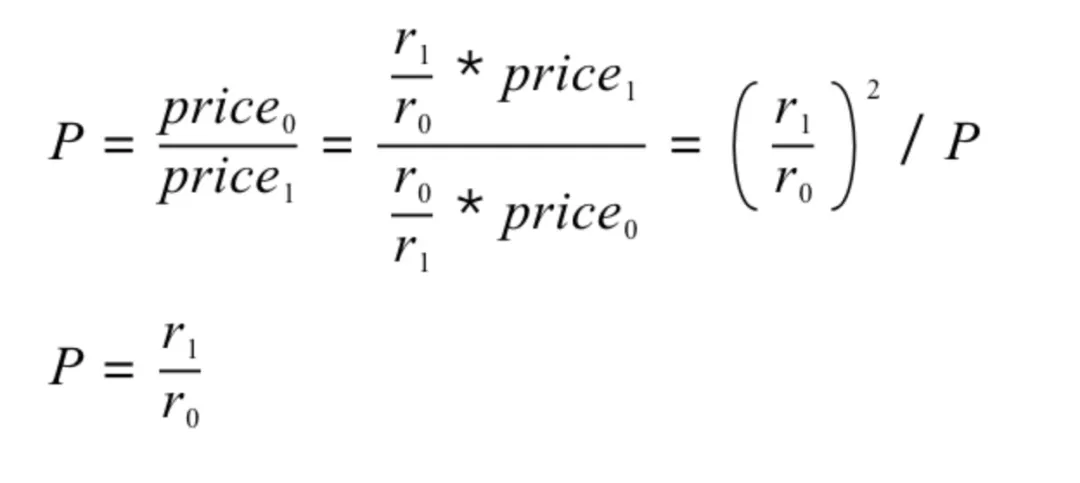
接着,根据 P 就可以倒推真实的 r0,r1,如下:
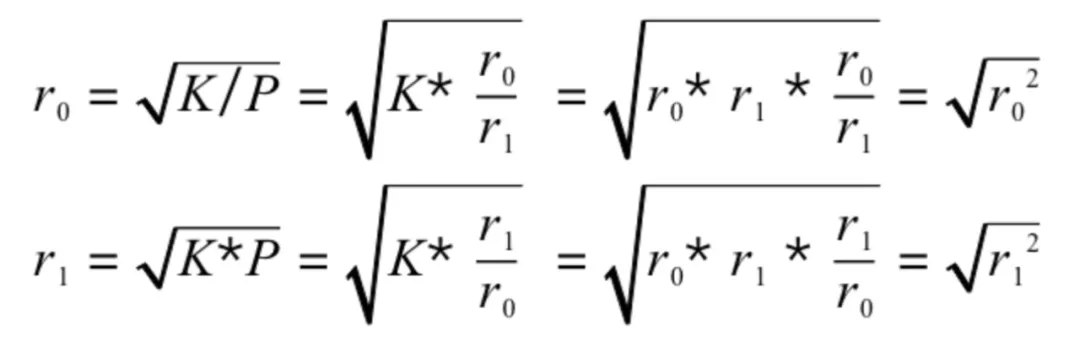
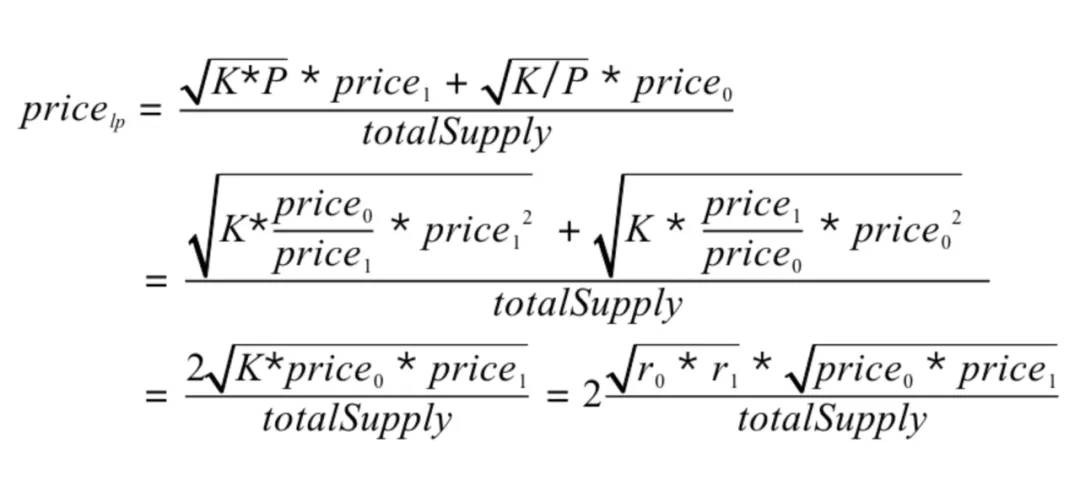
那么,拿到了正确比例的 x 和 y 之后,LP 的价格会是下面这个公式:
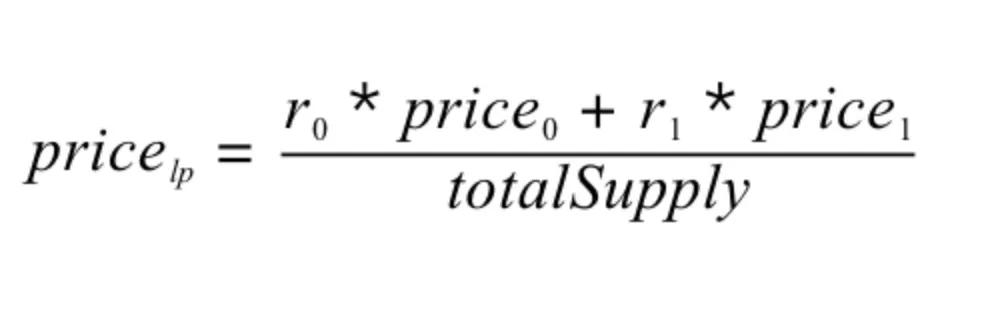
再转换成如下:
攻击的可能性
在完成公式分析后,我们不难知道,只要有正确的价格的比例 P,就能根据这个比例倒推真实的 r0 和 r1,最后得到公式:
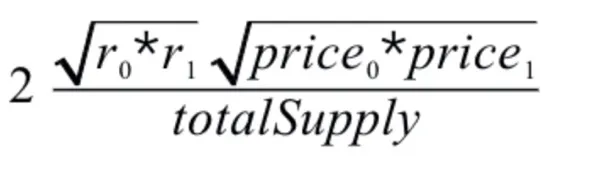
那么,这个公式能不能被攻击呢?从公式上可以知道,公式的 price0,price1 都是可信源获取的正确的价格,这个值是无法被操控的,然后是 totalSupply,这个值虽然可以操控,但是在控制 LP 价格进行攻击的过程中改变 totalSupply 只能是改变你的抵押数量,这个暂时没有用。那么剩下可以操控的只有 r0 和 r1 的值了。如何改变 r0,r1 的值呢?下面提供两种思路进行分析:
思路一:直接进行代币兑换
我们知道,在代币池中,无论是采用什么算法进行计算,代币池在进行代币兑换的过程中,必然会发生代币数量的改变,那么这种改变最终能不能操控公式呢?其实是不可以的。我们知道,在恒定乘积的模型中,x * y = K 总是成立的,那么也就是说无论交易过程中怎么发生代币的兑换,K 的值总是不变的(这里不考虑手续费的情况),而公式中采用的是 r0 和 r1 进行相乘,所以使用代币兑换来操控公式实际上是不可行的。
思路二:将代币直接打入到代币池中
这种思路比较粗暴,可以直接忽视 K 值来操控 r0 和 r1 相乘的值,但是经过我的运算,这种方法看似可行,其实是不行的。虽然达到了操控的目的,但是因为公式本身在获取最终价格的时候采用的是根号的模式,所以最后获得的收益是根号后的收益,比方说付出 10,000 的成本,最后只能获得最多 100 的收益,这样是明显不划算的。所以这种思路也是不可行的。
适用范围
本算法的适用范围仅限于适用 AMM 模型的代币池的 LP 价格的获取,因为整个推导过程都基于恒定乘积公式中 K 的基本特性来进行。获取的 LP 本身所属的交易对算法不使用 AMM 模型是不可行的,因为这种情况下,前面所有的假设都已经不成立了,那么对应的公式的推算自然也是不成立的。
总结
LP 抵押已经成为了一种迫切的需求,在目前没有更好的方式(如 ChainLink 提供的 LP 喂价,Uniswap 提供延时 LP 接口等),Alpha Finance 的方式可以说是一种较为安全的实现方法,使针对数量进行控制的攻击变成不可行或成本非常高。当然,随着越来越多场景的出现,这种算法也不一定是万能的,项目方需要结合自身的场景,合理运用该算法,达到良好的效果。此外,特别需要注意的是,虽然公式的终极形式用的是开根号的 r0,r1 和 price0,price1 相乘,但是真正实现的时候,需要根据 K 来推导具体的 r0 和 r1 的值,不然会存在一定的误差。
参考链接:







